Mesh/Current Analysis

The technique of nodal analysis described in the preceding topic is completely general and can always be applied to any electrical network. This is not the only method for which a similar claim can be made, however. In general, we shall meet a generalized nodal analysis method and a technique known as loop analysis. Let us first consider a method known as mesh analysis. Mesh Method is perhaps the most popular technique used by engineers to solve complex circuit problems.

Even though this technique is not applicable to every network, it is probably used more often than it should be and it can be applied to most of the networks to be analyzed. Mesh analysis is applicable only to those networks which are planar, a term we hasten to define. The mesh is a property of a planar circuit and is not defined for a non-planar circuit. We define a mesh as a loop which does not contain any other loops within it.

Mesh Currents and Essential Meshes

Mesh analysis works by arbitrarily assigning mesh currents in the essential meshes. We define mesh current as a current which flows only around the perimeter of a mesh. The mesh current may not have a physical meaning but it used to set up the mesh analysis equations. To help prevent errors when writing out the equations, it is important to have all the mesh currents loop in the same direction when assigning the mesh currents. A mesh current is indicated by a curved arrow that almost closes on itself and is drawn inside the essential mesh.

Figure 1  Meshes in a Circuit

 

The convention is to have all the mesh currents looping in a clockwise direction because error-minimizing symmetry then results in the equations. Mesh analysis greatly simplifies the problem by ensuring that the least possible number of equations regarding currents is used. The current through any branch must be determined by considering the mesh currents flowing in every mesh in which that branch appears. That is not difficult because it is obvious that no branch can appear in more than two meshes.
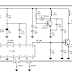
Example:

What is the voltage across the current source?

Figure 2  Example Circuit

Defining the mesh currents in the conventional way, the KVL equation for mesh 1 is:

KVL for mesh 2:

By inspection of mesh 3:

Subsequent elimination of  i3 in the mesh 2 equation leads to:

Adding the two equations immediately above produces:

Back substitution of i1 into one of the equations involving both i1 and i2 produces:

As a straightforward way to find the voltage across the current source is to evaluate the voltage across the 5 Ohm resistor. The current through the resistor is i2 - i3 = 0.78A, thus the voltage across the resistor must be (0.78 A) (5 ohm) = 3.89 V.

Source : http://www.eeweb.com/blog/andrew_carter/mesh-analysis